CSCI C343 Data Structures Spring 2025
Lab: Linked Lists
Overview
For this lab, you will write and test several functions with linked lists in the Deduce programming language.
Table of Contents
- Deduce Setup
- Problem Set
- Sum
- Concatenation
- Quick Reverse
- Cumulative Sum
- Search
Deduce Setup
Installation
The following instructions are how we recommend setting up deduce development for the class, you can find more detailed information on the deduce website.
- The first thing you should do is install deduce itself. Download and extract the zip file from github.
- Open the resulting folder in visual studio code, which you can install here.
-
Navigate to the extensions menu, and search for and install the deduce-mode extension. This makes it easier to run deduce files and gives you syntax highlighting, as well as some basic autocomplete options.
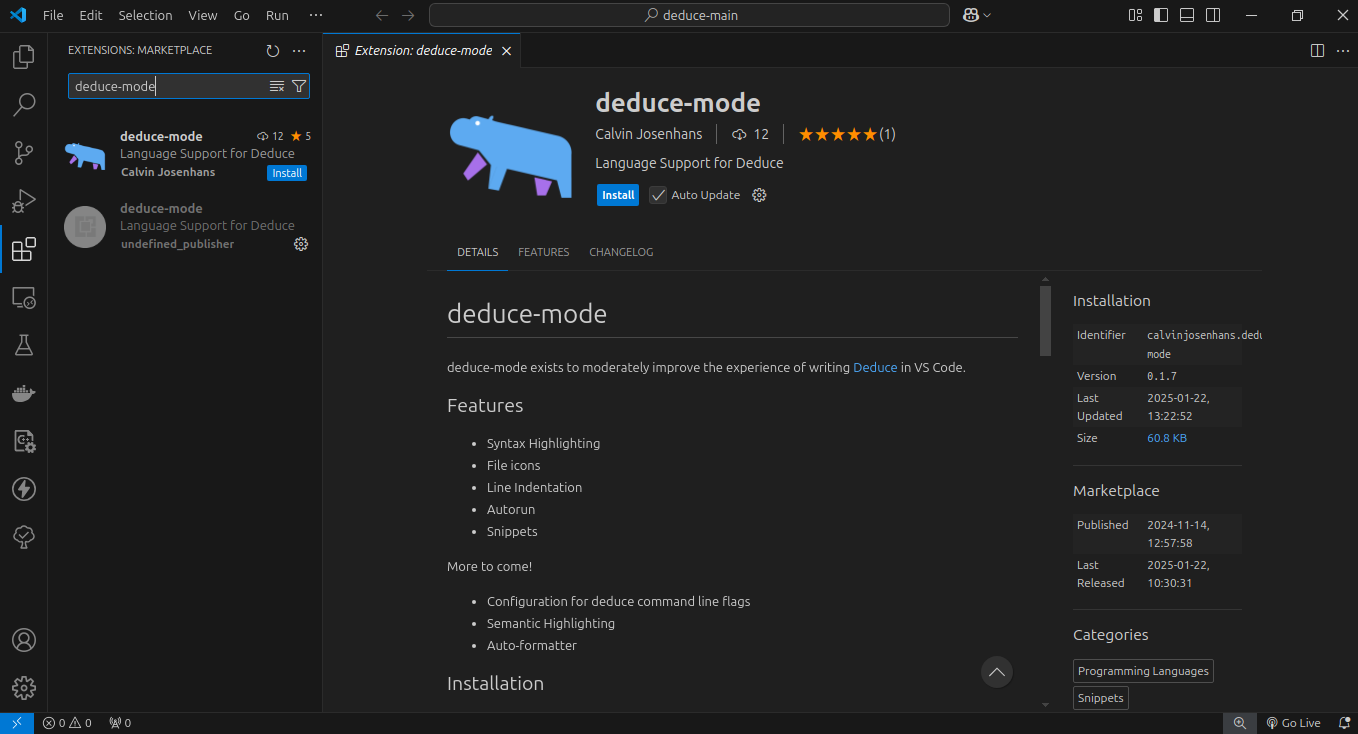
- Create a new folder called
343in the deduce directory, where you can keep your work for this class. - In the 343 folder, create a file named
hello.pf. This is your first deduce script! - Paste the following code block into the newly created file.
import Nat define hello = 42 print hello - Now you should be able to click the deduce icon at the top right of your window
and run the file!
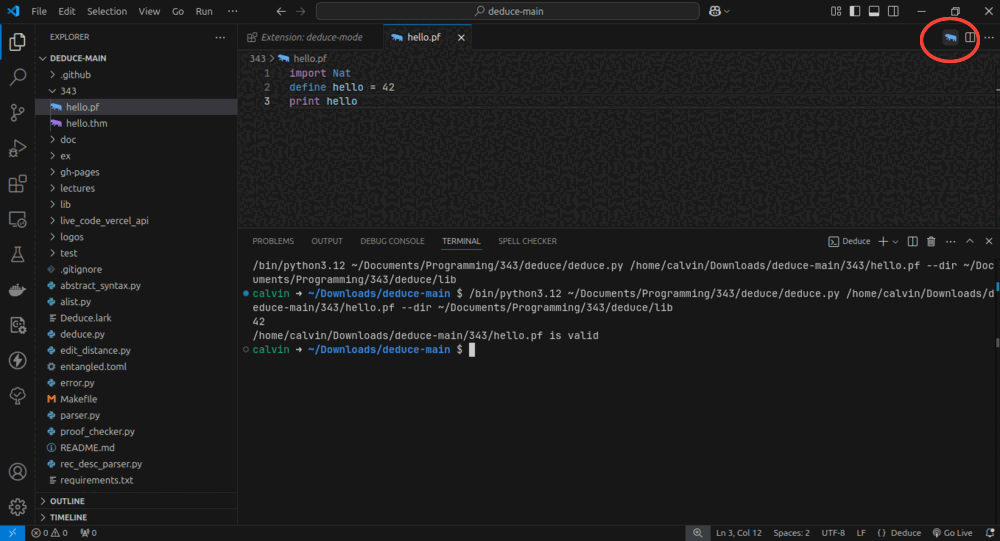
- You will probably see some error in the terminal that falls into one of
two categories.
- If you see
ModuleNotFoundError: No module named 'lark.tree', you need to install a missing Python package that deduce relies on. Try runningpython -m pip install larkin the terminal. If this works, great! If not, an instructor can help. - Otherwise, you likely don’t have Python installed. Download and run the installer from python.org. Then add the Python extension to vscode, much as you did for deduce-mode.
- If you see
- If you encounter another error or these steps don’t work, an instructor can help you get things working.
-
If everything went correctly, you should see this in the terminal
42 hello.pf is valid
Problem Set
Complete the following exercises in a file named LabDeduceProgramming.pf.
Then submit the file to the
autograder.
Before submitting, you can also write your own tests using assert statements
for each of the functions you write.
Sum the elements of a List
Create a function named sum that adds up the elements of a list. In
particular, the elements are natural numbers, so they have type Nat.
You will need to import the type Nat and operations, such as
operator +, from Nat.pf, with the following import statement.
import Nat
You’ll also need to import the List library.
import List
Here’s the skeleton for your sum function.
function sum(List<Nat>) -> Nat {
FILL IN
}
The following shows an example use of the sum function.
assert sum([1,2,3,4]) = 10
Concatenating a List of Lists
Create a function named concat that turns a list-of-lists into a
list. The concat function should have the following type.
concat : < E > fn List<List<E>> -> List<E>
In general, you may use any functions in List.pf.
The following shows an example use of the concat function.
assert concat([[1,2,3], [4,5]]) = [1,2,3,4,5]
Use this assert statement and several of your own to test whether
your concat function behaves as expected.
Quick Reverse, Accumulator-Passing Style
The reverse function in List.pf is O(n²) time because it invokes
append (operator ++) n times and append is O(n). Create a
function named quick_rev that reverses the input list and that is
O(n) time. The quick_rev function should be generic and have the
following type.
quick_rev : < E > fn List<E> -> List<E>
Use assert statements to test whether your quick_rev function
really reverses the input.
Hint: we recommend that you create an auxilliary function that is written in accumulator-passing style.
Consider the sum function that you created above. We can change
sum to accumulator-passing style by adding an extra parameter that
stores the total-so-far.
function sum_accum(List<Nat>, Nat) -> Nat {
sum_accum(empty, total) = total
sum_accum(node(x, xs), total) = sum_accum(xs, x + total)
}
(One side benefit of accumulator passing style is that the function is
tail recursive, which means that it uses O(1) space on the procedure
call stack, whereas sum uses O(n) space.)
assert sum([1,2,3]) = sum_accum([1,2,3], 0)
Cumulative Sum of a List
The cumulative sum of a list of numbers produces a list where each element is the sum of all the elements of the input list up to and including the index of the current element. So if the input list is
n0, n1, n2, ...
the output list is
n0, n0+n1, n0+n1+n2, ...
Create a function named cumulative_sum that performs this operation.
The cumulative_sum function should have the following type.
cumulative_sum : List<Nat> -> List<Nat>
Here is an example of using the cumulative_sum function.
assert cumulative_sum([3,1,5,2,4]) = [3,4,9,11,15]
Test your cumulative_sum function with several more assert
statements.
Search (Variant)
Fill in the definition of the following variant of linear search.
This search function separates the input list into two lists, the
first list does not contain the given number, and the second list
starts with the given number. If the given number is not in the input
list, then the first list is the entire input list and the second list
is empty. To return two lists, use the Pair type which you can
import from the Pair library.
function search(List<Nat>, Nat) -> Pair<List<Nat>, List<Nat> > {
FILL IN
}
Here are some example uses of this search.
define list_123 = [1,2,3]
assert search(list_123, 1) = pair([], [1,2,3])
assert search(list_123, 2) = pair([1], [2,3])
assert search(list_123, 3) = pair([1,2], [3])
assert search(list_123, 4) = pair([1,2,3], [])