CSCI H343 Data Structures Fall 2024

Lecture: Graphs and Breadth-first Search

The standard mathematical way to represent a graph G is with a set of vertices V and a set of edges E, that is, G = (V,E).

In a directed graph, each edge is a pair of vertices where the first vertex is called the source and the second is the target.

In an undirected graph, each edge is a set containing two distinct vertices.

I often use n for the number of vertices and m for the number of edges.

The following is an example of a directed graph.

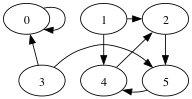
**Example of a directed graph.**

The set of vertices for this graph is

{0,1,2,3,4,5}.

The set of edges is

{(0,0), (1,2),(1,4),  (2,5),  (3,5),(3,0),  (4,2),  (5,4),  }.

The following is an undirected graph.

**Example of an undirected graph.**

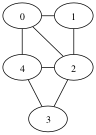
The set of vertices is {0,1,2,3,4}.

The set of edges is { {1,2},{1,0}, {2,3},{2,4},{2,0}, {3,4}, {4,0} }.

We often writes an undirected edge as (1,2) or 1-2 instead of {1,2}.

Adjacency List

The Adjacency List representation of a graph is an array of linked lists.

Example: for the above directed graph the adjacency list representation is

 |0| -> 0
 |1| -> 2 -> 4
 |2| -> 5
 |3| -> 0 -> 5
 |4| -> 2
 |5| -> 4

Example: for the above undirected graph the adjacency list representation is

 |0| -> 1 -> 2 -> 4
 |1| -> 0 -> 2
 |2| -> 1 -> 4 -> 3 -> 0
 |3| -> 2 -> 4
 |4| -> 0 -> 3 -> 2

(Each edge is stored twice.)

Adjacency lists are good for storing sparse graphs.

Space: O(n + m).
Edge detection given two vertices: O(n)
Edge insert: O(1)
Edge removal given two vertices: O(n)
Edge remove given edge handle: O(1) if use double linked
Edge removal: O(n) or O(1) if use double linked and edge handle
Vertex insert: amortized O(1)
Vertex delete: not easily supported

Adjacency Matrix

The Adjacency Matrix representation of a graph is a Boolean matrix.

Example, for the directed graph above.

1 2 3 4 5
1 0 0 0 0 0
0 0 1 0 1 0
0 0 0 0 0 1
1 0 0 0 0 1
0 0 1 0 0 0
0 0 0 0 1 0

Example, for the undirected graph above.

Note that the matrix is symmetric.

Adjacency matrices are good for dense graphs.

Space: O(n²)
Edge detection given two vertices: O(1)
Edge insert: O(1)
Edge removal given two vertices: O(1)
Edge remove given edge handle: O(1)
Edge removal: O(1)
Vertex insert: amortized O(n)
Vertex delete: not easily supported

How could we represent Adjacency Matrices in Java?

Breadth-First Search

Def. a path is a sequence of edges such that the target of each edge matches the source of the next edge in the sequence. We sometimes abbreviate a path to v₀ ⇒ vₖ, where v₀ is the source of the first edge and vₖ is the target of the last edge. We write v₀ ⇒ᵏ vₖ when the length of the path is important. Also, when talking about multiple different paths, we might use a subscript to give the path a name, such as v₀) ⇒ₓ vₖ.

Problem: compute the shortest paths from vertex g to all other vertices in the graph.

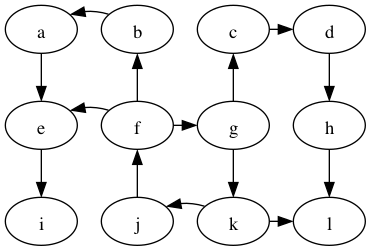
**Compute shortest paths from vertex g.**

Example: what is a shortest path from g to f?

Possible solution: g → k → j → f, length 3.

To prove this is really the shortest, we need to make sure there are no paths of length less-than 3 from g to f.

How do we prove that? Well, look at all paths of length less-than 3 that start from g.

Length 0 paths:

Length 1 paths:

g → c

g → k

Length 2 paths:

g → c → d

g → k → l

g → k → j

Good, none of the paths from g with length less-than 3 reach f.

So indeed, g → k → j → f is the shortest path from g to f.

BFS Algorithm

Towards a general algorithm for BFS, can we compute all the k+1 length shortests paths given all the k-length shortest paths?

Draw a picture of the wave-front of the k-length shortest paths and the out-edges on the wave-front.

High-level Algorithm:

for k = 0...n
  for each path s ⇒ᵏ u:
	for each edge {u,v} incident to u:
	  If we don't already have a shortest-path to v, 
	  then s ⇒ᵏ⁺¹ u is a shortest path from s to v.

What data structures should we use?

The shortest paths form a tree: for each vertex v, store the previous vertex u in its shortest path. we call u the “parent” of v because u is the parent of v in the tree of shortest paths. This is also called the breadth-first tree.
For the paths of length k: We just need the end vertex of each path, so let’s maintain a bag of the vertices at the ends of the paths of length k.
To make sure we ignore vertices that have already been encountered, we use an array called done that maps vertex numbers to True/False.

Version 1 of the algorithm

static <V> void
bfs_v1(Graph<V> G, V start, Map<V,Boolean> visited, Map<V,V> parent) {
	for (V v : G.vertices())
		visited.put(v, false);
	int k = 0;
	ArrayList<V> ends = new ArrayList<V>();
	ends.add(start);
	parent.put(start, start);
	visited.put(start, true);
	while (k != G.num_vertices()) {
		ArrayList<V> new_ends = new ArrayList<V>();
		for (V u : ends) 
			for (V v : G.adjacent(u))
				if (! visited.get(v)) {
					parent.put(v, u);
					new_ends.add(v);
					visited.put(v, true);
				}
		ends = new_ends;
		++k;
	}
}

Some observations about version 1

If the new_ends is empty at the end of the loop body, then we can stop early.
The ends and new_ends can be combined into a single data structure if we use a queue instead of two bags.

The front part of the queue represents ends and the back part of the queue represents new_ends.

With this change, we can simplify the code by combining the while k and the for u loops into a single loop that checks whether the queue is non-empty.

Final version of breadth-first search

static <V> void
bfs(Graph<V> G, V start, Map<V,Boolean> visited, Map<V,V> parent) {
	for (V v : G.vertices())
		visited.put(v, false);
	Queue<V> Q = new LinkedList<V>();
	Q.add(start);
	parent.put(start, start);
	visited.put(start, true);
	while (! Q.isEmpty()) {
		V u = Q.remove();
		for (V v : G.adjacent(u))
			if (! visited.get(v)) {
				parent.put(v, u);
				Q.add(v);
				visited.put(v, true);
			}
	}
}

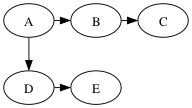
Student group work

Example run of BFS version 2, start at node A.

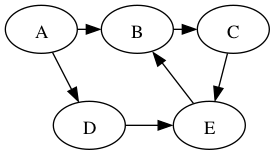
**BFS exercise.**

queue       parents
[A]         P[A] = A
[B,D]       P[B] = A, P[D] = A
[D,C]       P[C] = B
[C,E]       P[E] = D
[E]
[]

**Solution: a BFS tree.**

Time complexity of BFS

Main loop: we traverse the entire adjacency list graph once and the combined length of the adjacency lists is O(m), so we have O(m) for the main loop.
Initialization: O(n) time and space for the parent and done arrays.
Total: O(n + m)