CSCI H343 Data Structures Fall 2024
Lab: Array Search and Testing
Overview
Welcome to CSCI-C343 “Data Structures”!
In this lab, we will first go through software installation and review basic testing and debugging skills. You will then be asked to implement three array search algorithms. Finally, you are supposed to create test cases for those algorithms and submit both your code and your test cases to Autograder.
Table of contents:
- Software Installation
- Instructor Demonstration: Testing and Debugging
- Task 1: Implementing Array Search
- Task 2: Testing Array Search
- Submission and Grading
Software Installation
- Download and install IntelliJ IDEA Community Edition
- Alternatively, you may use a package manager such as Homebrew:
brew install intellij-idea-ce - Software like IntelliJ is often referred to as IDEs, because they integrate a code editor, build tools and a debugger.
- Alternatively, you may use a package manager such as Homebrew:
- Launch the IntelliJ IDE
- In the welcome window, click “New Project”.
In general, we create a new project for each lab. Sometimes a project code
skeleton is provided to you; in that case, you can use the “Open” button
to choose the root directory of that project.
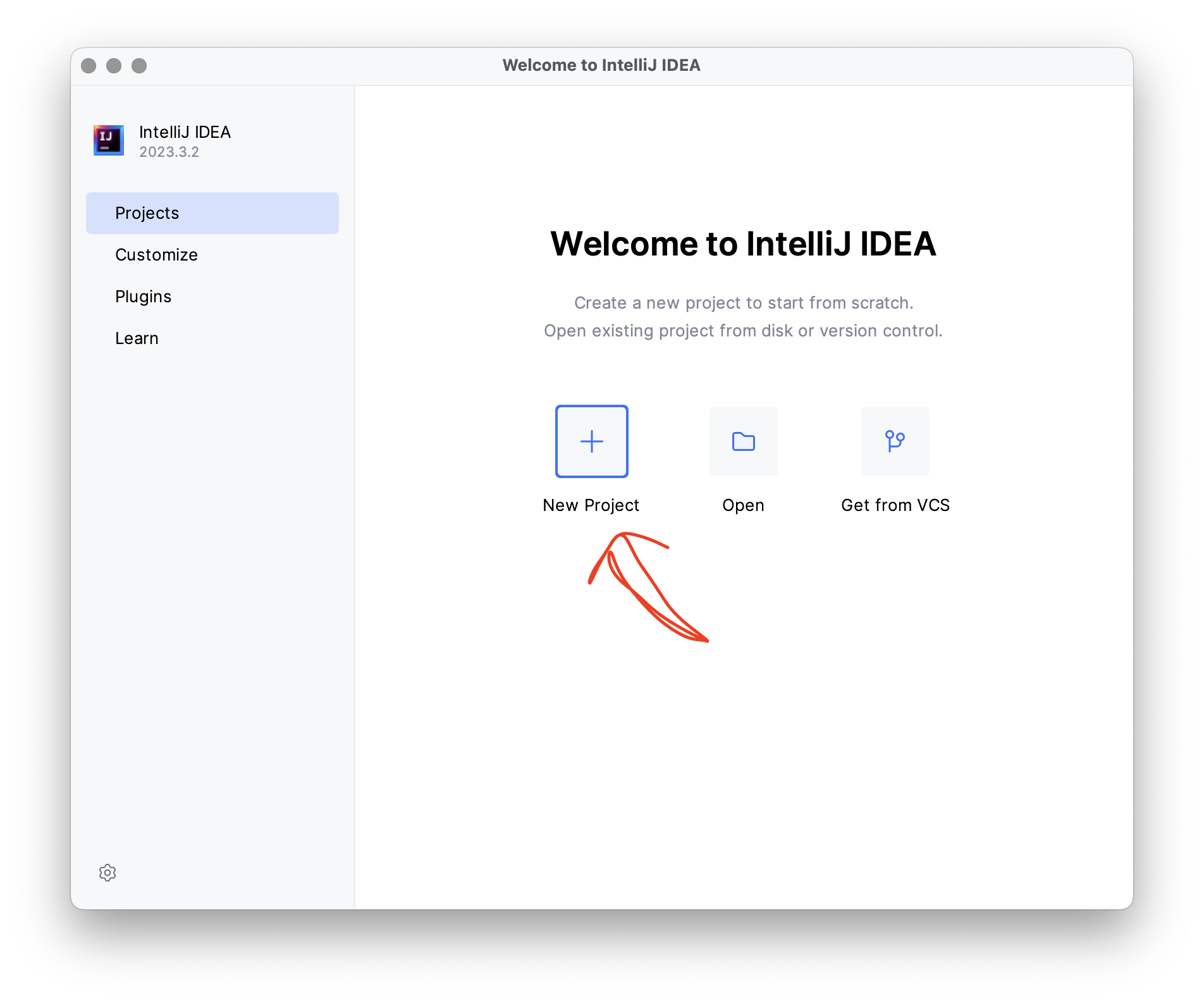
- In the pop-up window, enter the title of your lab assignment as “Name”.
For this lab, it should be
Search. - Choose “Location”, which is whatever directory that you prefer to contain all lab assignments. (Optional: ) check “Create Git repository” if you would like to use version control.
- Language: “Java”; build systems: “IntelliJ”
- Install JDK. Click “Add SDK -> Download JDK” in the “JDK” drop-down menu:
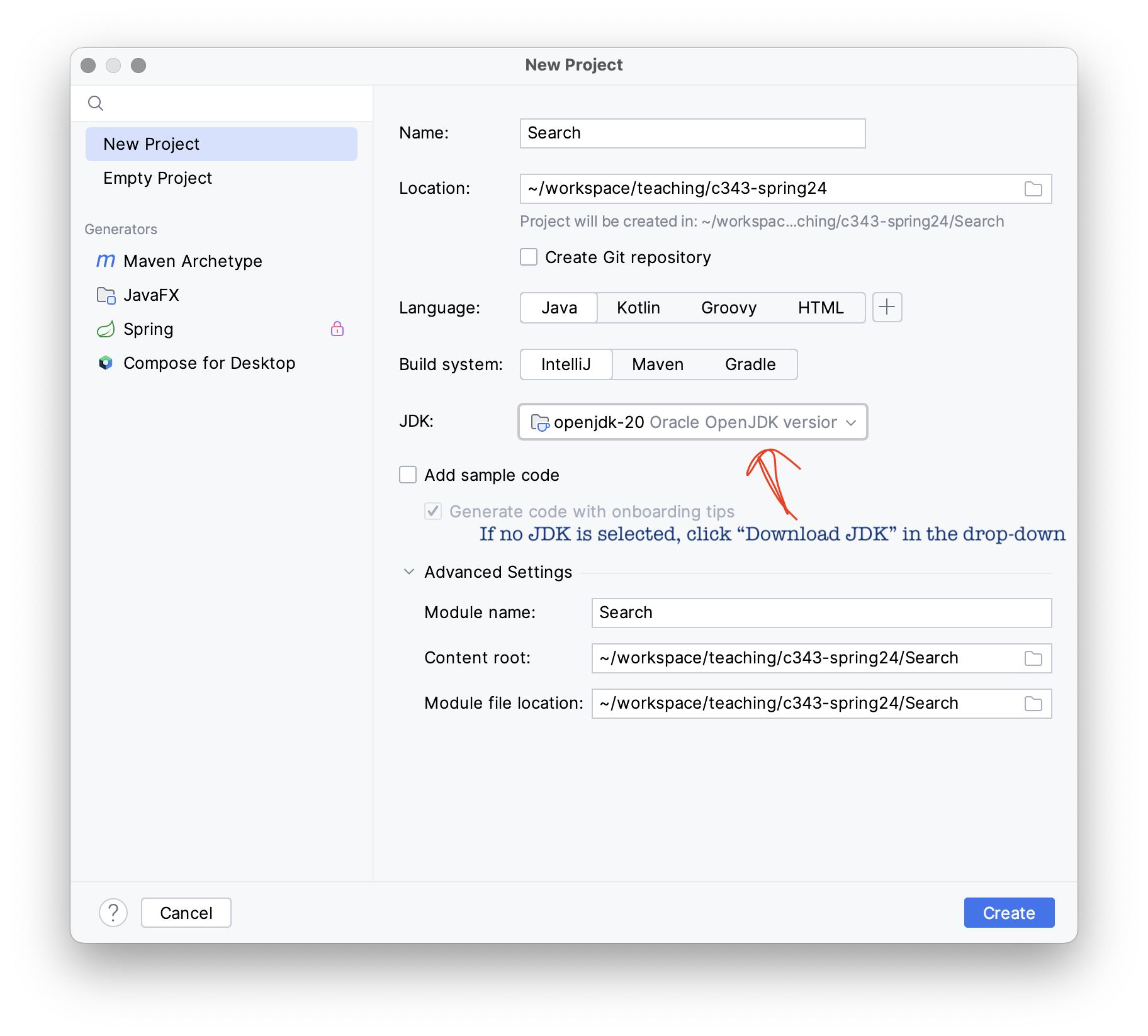
- In the pop-up window choose “Vendor” : “Oracle OpenJDK”. “Version” should
be filled in automatically (make sure version ≥15). “Location” can be left as default.
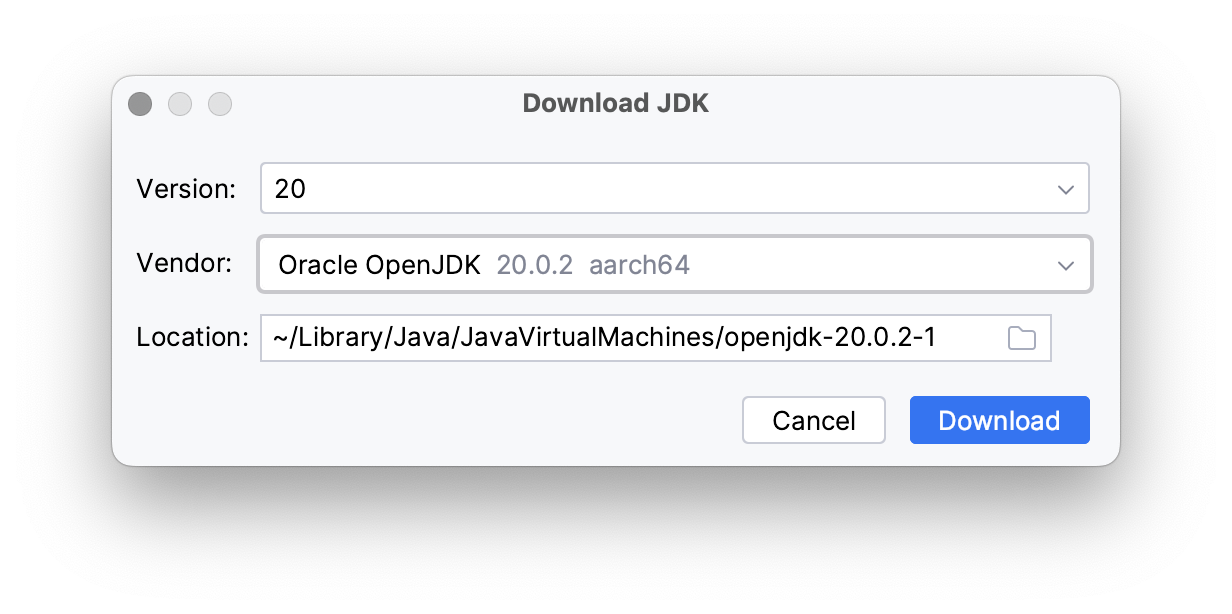
- Click “Download” and wait for the download to finish. In the “New Project” window, uncheck “Add sample code” and leave everything else as is. Click “Create”.
- In the welcome window, click “New Project”.
In general, we create a new project for each lab. Sometimes a project code
skeleton is provided to you; in that case, you can use the “Open” button
to choose the root directory of that project.
Instructor Demonstration: Testing and Debugging
In this section I will show you how to:
- Structure your lab projects
- Build and run the code
- Debug and test
The code for this demo is available here.
Suppose our tasks are to implement, test and debug the “ripple” approach of array rotation (recall lecture). We first create an IntelliJ project called “Rotation”. The file structure looks like:
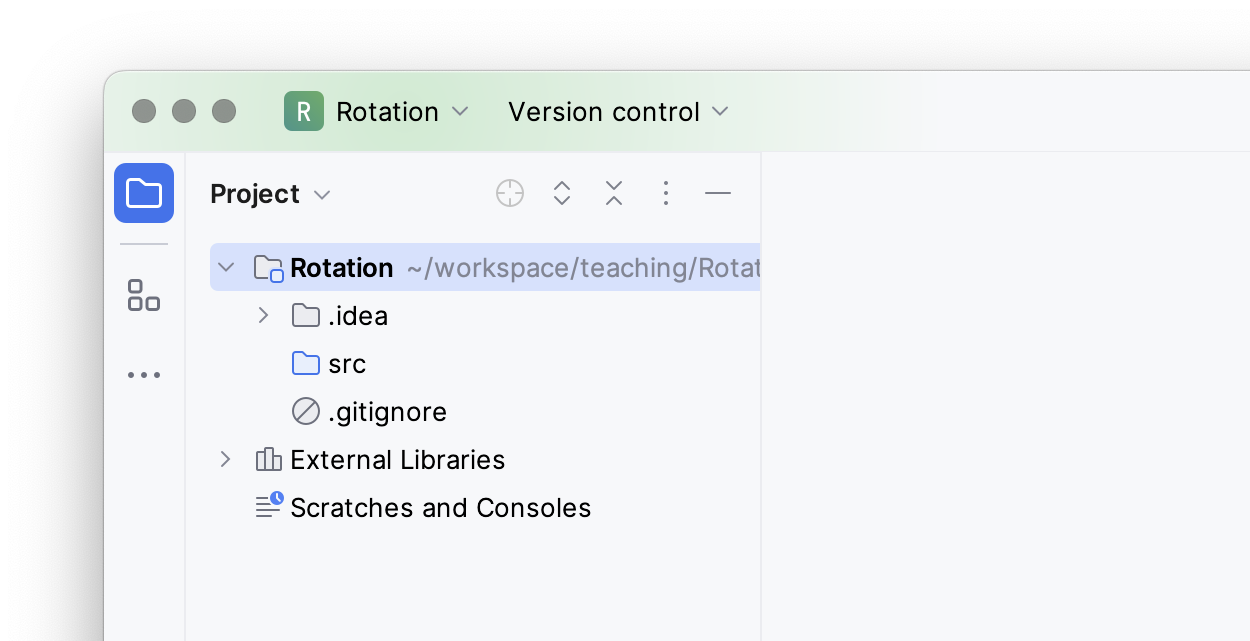
To create the Java class file where our implementation code resides, we right click
on the src directory and choose “Java Class”:
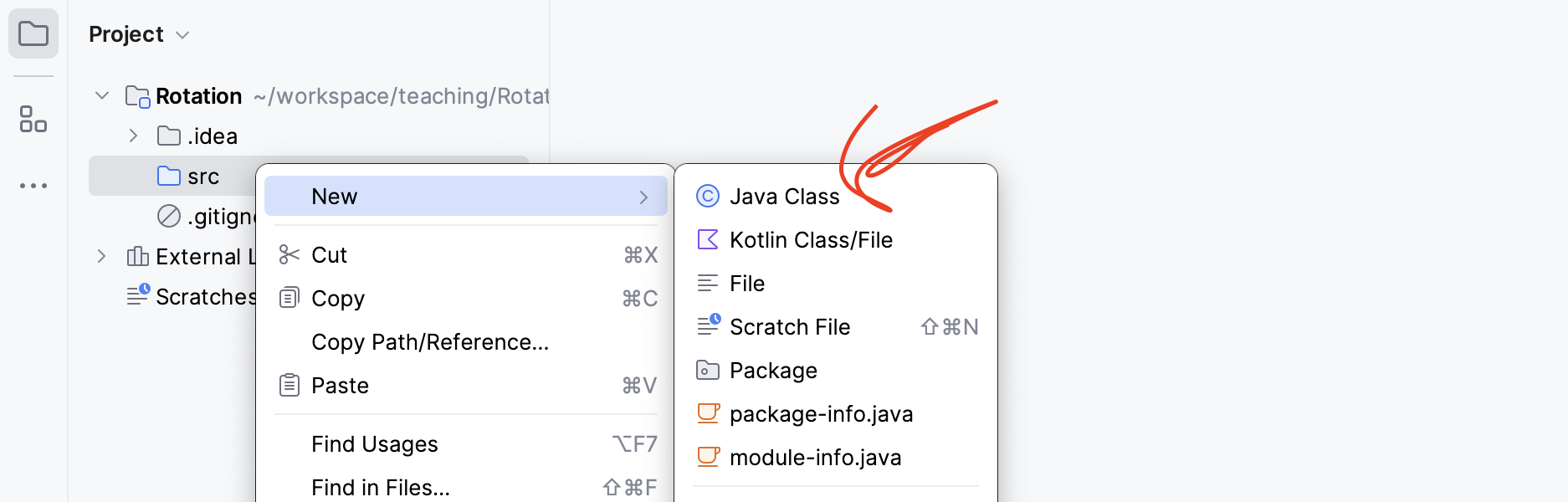
We enter “Rotation” as its name. IntelliJ creates a new file src/Rotation.java whose
content is an empty public class Rotation. In the editor, we create rotate_ripple
as a public static member function of Rotation:
public class Rotation {
public static void rotate_ripple(int[] A) {
if (A.length > 1) {
int tmp1 = A[0];
for (int i=0; i != A.length - 1; ++i) {
int tmp2 = A[i+1];
A[i+1] = tmp1;
tmp1 = tmp2;
}
A[0] = tmp1;
}
}
}
Our next task is to create unit tests for rotate_ripple. Right click on the root
directory and select “New -> Directory”. Name the new directory test.
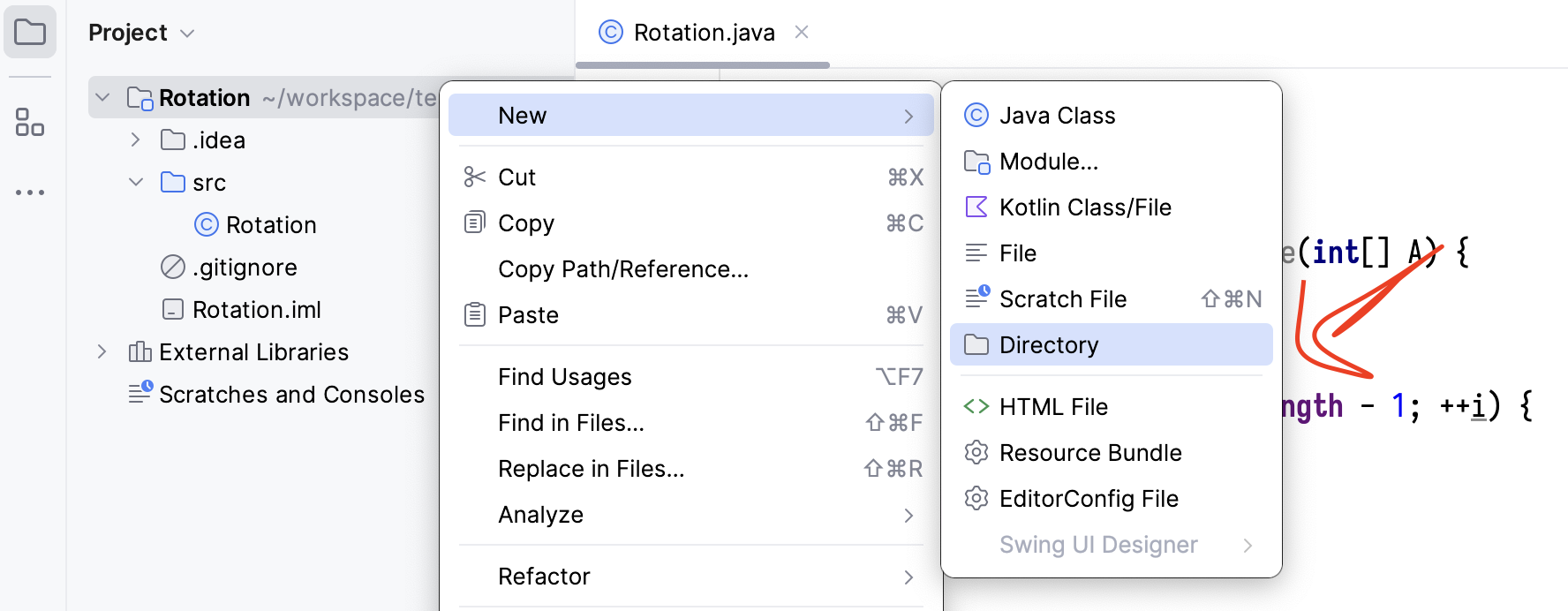
Right click on test in the file structure. Go to the last item in the pop-up menu
and select “Mark Directory As -> Test Sources Root”. The test directory will be
highlighted in green.
Create a new Java class file in test called RotationTest. Create rotate_save_n_shift
as a private static member function of RotationTest. We use rotate_save_n_shift
as our test oracle.
A test oracle is a mechanism for determining whether a test has passed or failed.
In this case, we are testing rotate_ripple against rotate_save_n_shift.
Next we import JUnit, a Java testing framework. Add the following
lines to the beginning of RotationTest:
import org.junit.jupiter.api.Test;
import static org.junit.jupiter.api.Assertions.*;
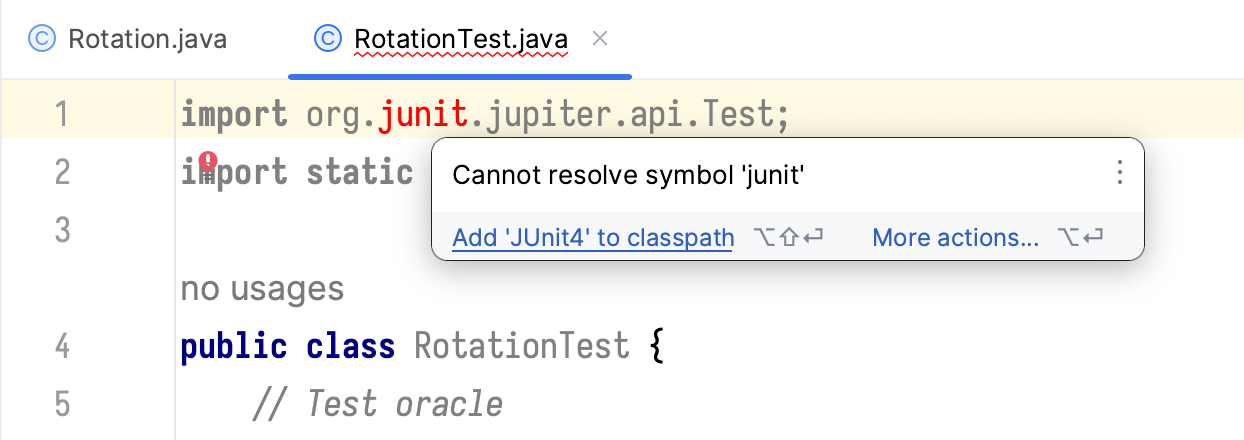
Careful readers may observe that some of the symbols are marked in red.
Move cursor to junit, where IntelliJ tells me that it cannot resolve the symbol.
Click on “Add ‘JUnit’ to classpath” and then “OK”. Perform the same action on jupiter.
Add the following as a public member function of RotationTest:
@Test
public void test_rotation_simple() {
String test_description = "rotating a small array";
int[] A = {1, 2, 3, 4, 5};
int[] B = {1, 2, 3, 4, 5};
rotate_save_n_shift(A);
Rotation.rotate_ripple(B);
try {
assertArrayEquals(A, B);
} catch (Exception e) {
fail(test_description + e.toString());
}
}
Note that the function is marked with the @Test attribute, which indicates
that it contains a unit test.
The array {1, 2, 3, 4, 5} is the example that we talked about in lecture.
We call the two implementations of rotation and compare the produced arrays
using assertArrayEquals, which is wrapped in a try-catch block. Should the
assertion fail, the catch clause throws an exception, which contains an error
message that consists of description of the test case and the exception e.
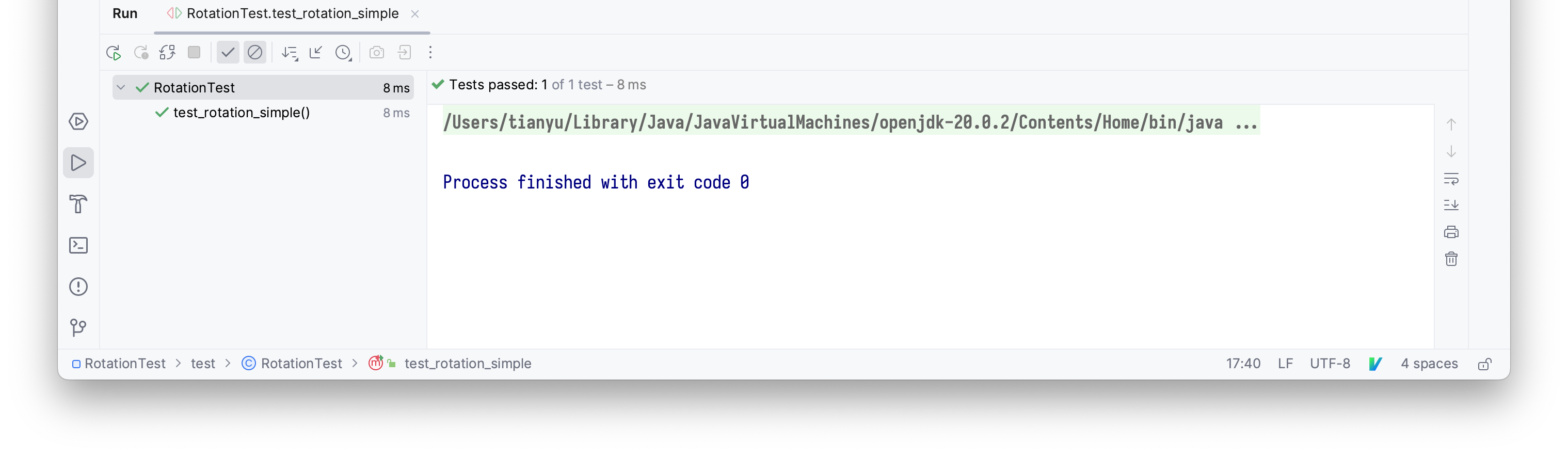
We can run this test point by clicking on the green icon:
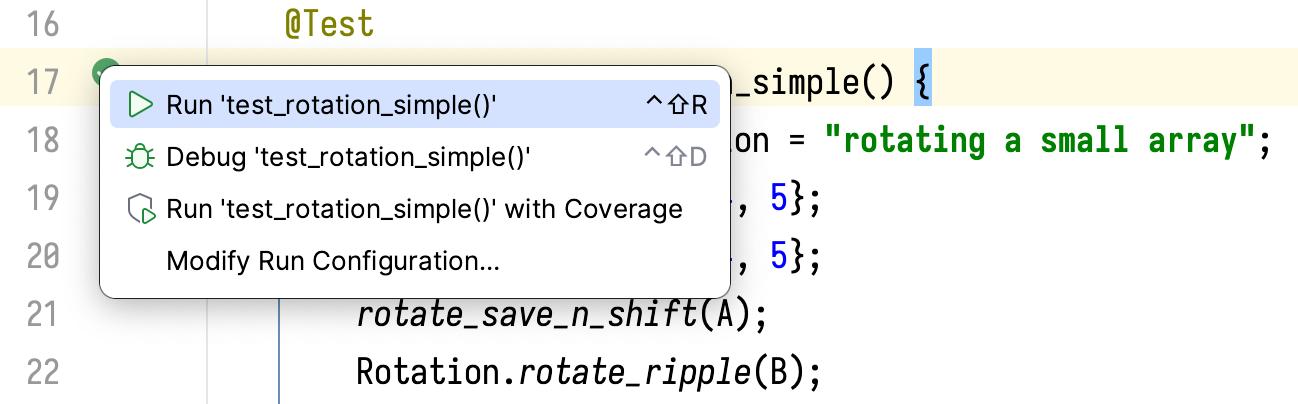
The rotation implementation is correct, so the test case passes:
We can also generate random numbers to fill the input array:
@Test
public void test_rotation_random() {
String test_description = "rotating an array with random integers";
Random r = new Random();
int[] A = new int[100];
for (int i = 0; i != A.length; ++ i) {
A[i] = r.nextInt();
}
int[] B = Arrays.copyOf(A, A.length);
rotate_save_n_shift(A);
Rotation.rotate_ripple(B);
try {
assertArrayEquals(A, B);
} catch (Exception e) {
fail(test_description + e.toString());
}
}
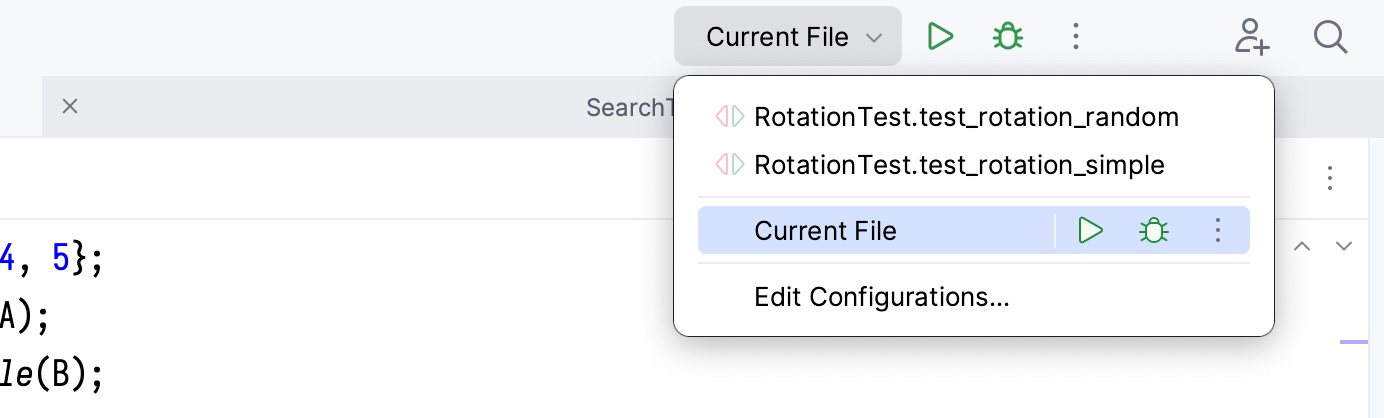
Now that we have multiple test cases, we can select which tests to run using the drop-down menu in the top-right corner:
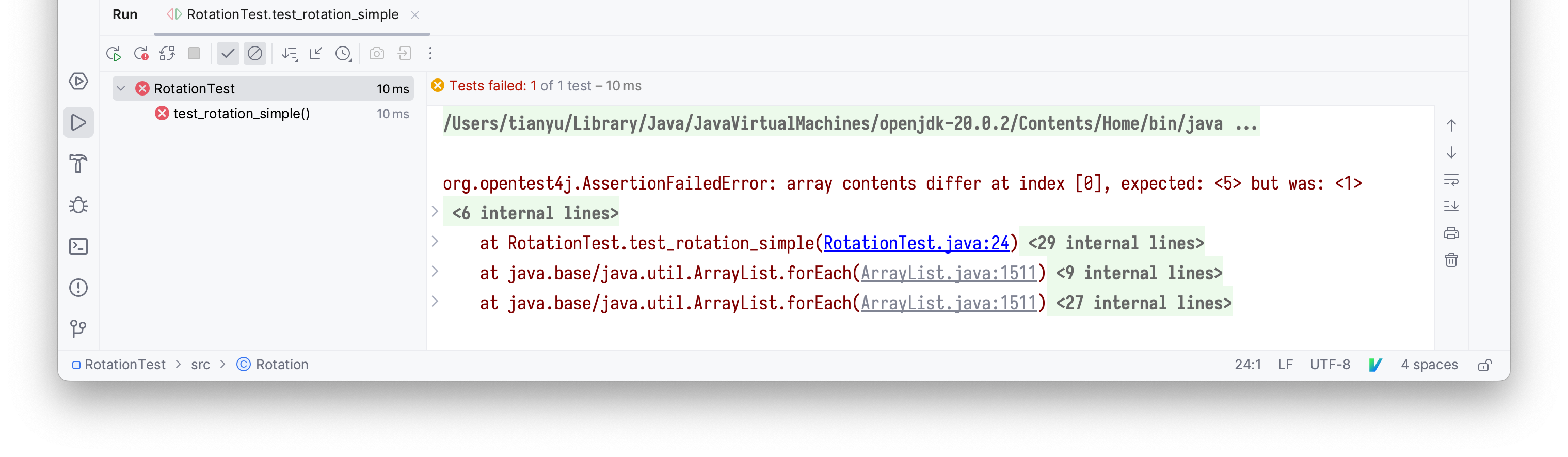
Suppose I made a mistake in the implementation. For example, if I did not assign tmp2
to tmp1, it would cause the entire array to be filled with A[0] and produce a wrong
answer. If we remove tmp1 = tmp2 and rerun the test, it catches the bug by throwing
an assertion error:
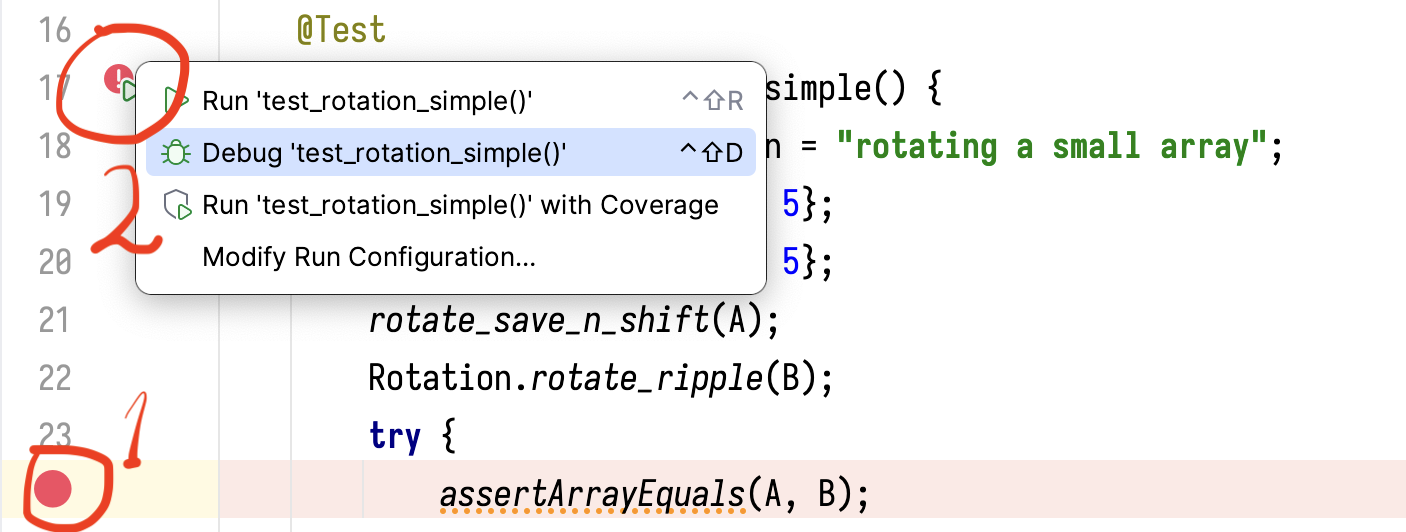
Now suppose we would like to debug the issue. We start by inspecting the two rotated arrays.
We can add a breakpoint at assertArrayEquals(A, B). We click on the line number and
it turns into a red dot. Then we choose “Debug …” from the drop-down menu:
Execution stops at the breakpoint. Both arrays, A and B, are displayed in the “Debug”
section of IntelliJ. We can see that the correct implementation produces {5, 1, 2, 3, 4} but
the buggy implementation produces {1, 1, 1, 1, 1} instead:
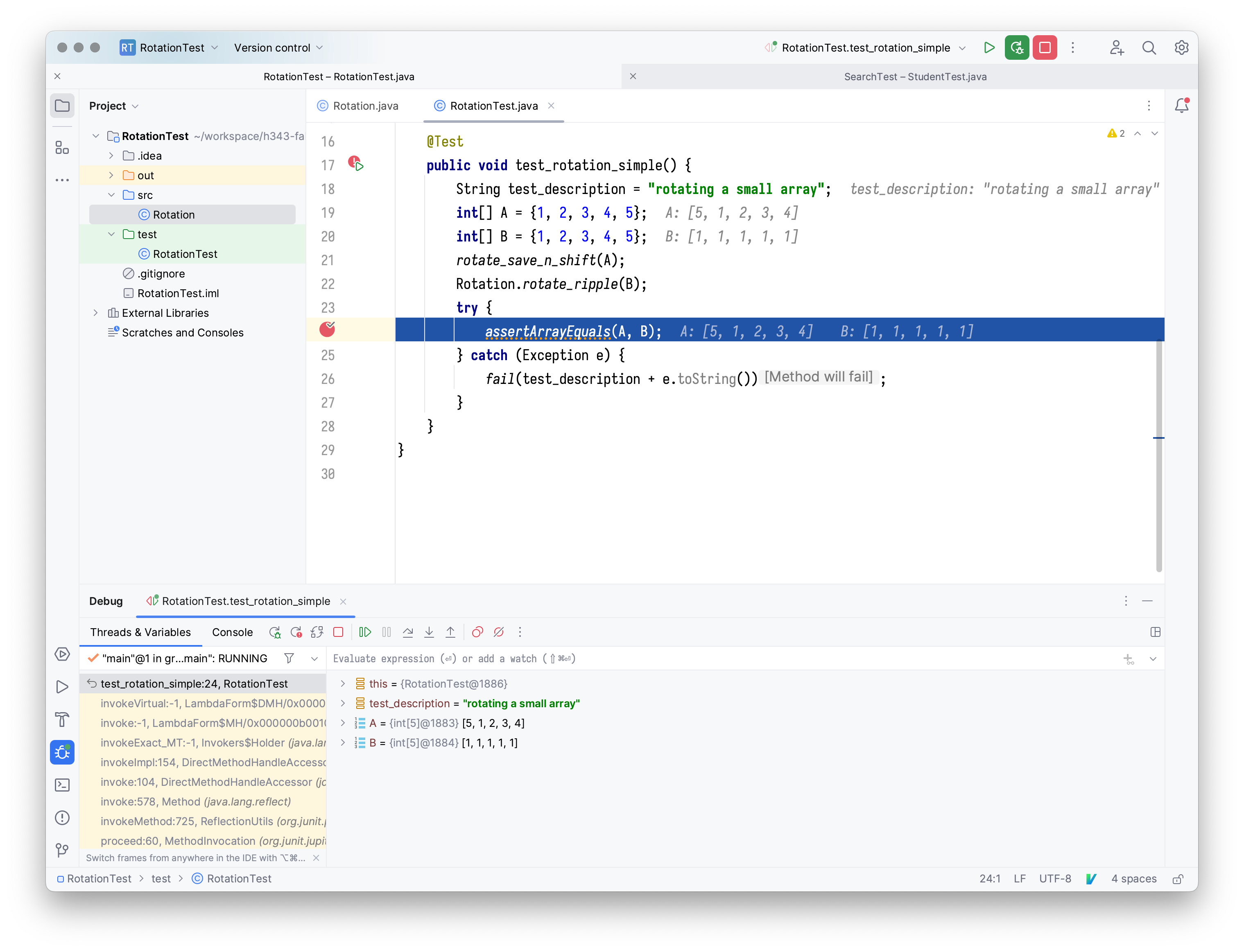
We can add more breakpoints by repeating the steps above. Breakpoints are controlled using the “View Breakpoints” pop-up (the two-overlapping-red-circles button). We can resume the execution by hitting the green play button (“Resume Program”). Alternatively, we can single-step through the program by pressing the down-arrow button.
Task 1: Implementing Array Search
Task Overview
In the first task, we are going to implement three search algorithms as
methods of a Java class called Search. Each of the algorithms finds
an element in the input array that meets certain criteria.
Create file src/Search.java which contains a public class called Search.
Implement each algorithm as a public function of the Search class.
Problem 1: Linear Search on an Array of Booleans
The most basic but surprisingly useful search function involves an
array A of boolean values (true or false).
Specification: The find_first_true(A, begin, end) function
returns the position of the first true in array A, that is, find
the smallest index i such that A[i] is true. The search is
restricted to the subarray within A that starts at the begin index
and finishes one element before the end index. (This is called a
half-open interval.) If there are no true elements in the subarray,
then find_first_true returns the end position of the subarray. The
caller of find_first_true is required to provide a valid half-open
range, which means begin <= end, 0 <= begin, begin <= A.length,
0 <= end, and end <= A.length.
The time it takes for your algorithm to run should be proportional to the
length of the array A.
[Example 1] If the input array A is
{false, false, true, false, true}
then the result should be 2 because A[2] == true and there are no
true elements at lower indices (A[0] and A[1] are both false).
[Example 2] Suppose A is the array
{true, false, true, false, true}
and we search in the half-open interval [1,3). The answer should be 2.
find_first_true(A, 1, 3) == 2
Add the following method to the Search class and fill-in the
implementation:
public static int find_first_true(boolean[] A, int begin, int end) {
// your code goes here
}
Problem 2: Linear Search on an Array of Integers
Another search function involves an array of integers.
Specification: The find_first_equal(A, x) function
searches on an array of integers A, with the goal of returning
the position of the first element in A that is equal to the x argument.
If there are no elements equal to x, the length of the array is returned.
⚠️ Use find_first_true to implement the function find_first_equal.
Again, the time it takes for your algorithm to run should be proportional
to the length of A.
[Example 3] Suppose A is the array
{32, 11, 4, 5, 99, 5, 32, 75}
then the result of search for 5 should be 3:
find_first_equal(A, 5) == 3
Implement the following method in the Search class:
public static int find_first_equal(int[] A, int x) {
// your code goes here
}
Problem 3: Binary Search on an Array of Booleans
We revisit searching an array of Booleans, but suppose that all of the
false elements in the array come before all of the true elements (sorted) this time.
Specification: The find_first_true_sorted(A, begin, end) returns
the position of the first true in array A, that is, it finds the
smallest index i greater or equal to begin and less than end
such that A[i] is true. If there is no true within the
half-open range [begin,end), it returns end. The caller must supply a
valid half-open range which means begin <= end, 0 <= begin, begin <= A.length,
0 <= end, and end <= A.length. Furthermore, the
array must already be sorted so that all the false elements come before any
true elements.
The algorithm should be more efficient and runs in time proportional to the ⚠️logarithm of the length of the array, by looking at the element in the middle and restricting the search to the right or left subarray depending on its value.
[Example 4] Suppose A is the sorted array
{false, false, true, true, true, true, true}
The position of the first true element is 2 in this case.
Implement your algorithm in the following method of the Search class.
Again, restrict your search to the half-open interval [begin,end):
public static int find_first_true_sorted(boolean[] A, int begin, int end) {
// your code goes here
}
Task 2: Testing Array Search
Task Overview
In Task 1 we have implemented three search functions. How do we know that those functions do what their specifications describe? In Task 2, you are supposed to create test cases for those three implementations. You have two options for test oracles: 1) using the Java standard library or 2) implementing your own. You are only responsible for testing correctness, not time complexity.
Think about the following questions before you start:
- What does it mean for each search algorithm to be correct? Hint: their specifications.
- Can some of the three algorithms share the same test oracle? Why?
- What are possible corner cases? Hint: arrays with 0 or 1 element, arrays with even or odd lengths, start and end positions being equal, …
Problem 4: Testing Three Search Functions
Create file test/StudentTest.java, which contains public class StudentTest.
Create your unit tests as methods of test/StudentTest.java.
If you come up with your own test oracles, they should go in
test/StudentTest.java as well.
The StudentTest class should contain a member function
public void test() (marked with @Test) which serves as the main entrance.
For example, if you have 2 test functions test_find_foo() and test_find_bar(),
the test() function should be:
@Test
public void test() {
test_find_foo();
test_find_bar();
}
Inside each test function, test_find_foo() or test_find_bar(), use JUnit’s
assertions
such as assertEquals to check for the correct answer.
[Example 5] Suppose we are testing
Search.find_first_true(A, begin, end) and the expected result is 2:
import org.junit.jupiter.api.Test;
import org.junit.jupiter.api.BeforeEach;
import static org.junit.jupiter.api.Assertions.*;
public class StudentTest {
@Test
public void test() {
test_find_first_true();
}
@Test
public void test_find_first_true() {
// ...
assertEquals(2, Search.find_first_true(A, begin, end));
}
}
Run the test cases. Does the result meet your expectation? Why?
Submission and Grading
In this course we use Autograder to provide instantaneous feedback to your lab submissions. Your grades will be decided by the number of test cases that your best submission passes. Multiple attempts are allowed.
- Submit
Search.javato link- You may submit your code an unlimited number of times.
- Autograder will run your submission on 8 test cases that thoroughly examine the correctness of all three search functions.
- Submit
StudentTest.javato link- You may submit your tests an unlimited number of times.
- Autograder will run your submission on 8 problematic
Searchimplementations. It also runs one correct implementation to rule out false positive. Your test cases are expected to throw exceptions on all implementations except the correct one.
- You have reached the end of the lab. Yay!