Lecture: Graphs and Topological Sorting

The standard mathematical way to represent a graph G is with a set of vertices V and a set of edges E, that is, G = (V,E).

In a directed graph, each edge is a pair of vertices where the first vertex is called the source and the second is the target.

In an undirected graph, each edge is a set containing two distinct vertices.

I often use n for the number of vertices and m for the number of edges.

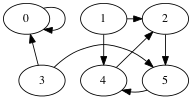
The set of vertices for this graph is

{0,1,2,3,4,5}.

The set of edges is

{(0,0), (1,2),(1,4),  (2,5),  (3,5),(3,0),  (4,2),  (5,4),  }.

Given edge (u,v) in a directed graph, we say v is adjacent to u. We sometimes write u to v for the edge (u,v).

The edge (u,v) is an out-edge of u and an in-edge of v.

The out-degree of a vertex is the number of its out-edges.

The in-degree of a vertex is the number of its in-edges.

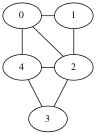
The set of vertices is {0,1,2,3,4}.

The set of edges is { {1,2},{1,0}, {2,3},{2,4},{2,0}, {3,4}, {4,0} }.

We often writes an undirected edge as (1,2) or 1-2 instead of {1,2}.

Given edge {u,v} in an undirected graph, we say u and v are adjacent to each other.

We say that edge {u,v} is incident on vertex u and v.

The degree of a vertex is the number of edges incident on it.

Adjacency List

The Adjacency List representation of a graph is an array of linked lists.

Example: for the above directed graph the adjacency list representation is

 |0| -> 0
 |1| -> 2 -> 4
 |2| -> 5
 |3| -> 0 -> 5
 |4| -> 2
 |5| -> 4

Example: for the above undirected graph the adjacency list representation is

 |0| -> 1 -> 2 -> 4
 |1| -> 0 -> 2
 |2| -> 1 -> 4 -> 3 -> 0
 |3| -> 2 -> 4
 |4| -> 0 -> 3 -> 2

(Each edge is stored twice.)

Adjacency lists are good for storing sparse graphs.

• Space: O(n + m).
• Edge detection given two vertices: O(n)
• Edge insert: O(1)
• Edge removal given two vertices: O(n)
• Edge remove given edge handle: O(1) if use double linked
• Edge removal: O(n) or O(1) if use double linked and edge handle
• Vertex insert: amortized O(1)
• Vertex delete: not easily supported

Adjacency Matrix

The Adjacency Matrix representation of a graph is a Boolean matrix.

Example, for the directed graph above.

  0 1 2 3 4 5
0 1 0 0 0 0 0
1 0 0 1 0 1 0
2 0 0 0 0 0 1
3 1 0 0 0 0 1
4 0 0 1 0 0 0
5 0 0 0 0 1 0

Example, for the undirected graph above.

  0 1 2 3 4
0 0 1 1 0 1
1 1 0 1 0 0
2 1 1 0 1 1
3 0 0 1 0 1
4 1 0 1 1 0

Note that the matrix is symmetric.

Adjacency matrices are good for dense graphs.

• Space: O(n²)
• Edge detection given two vertices: O(1)
• Edge insert: O(1)
• Edge removal given two vertices: O(1)
• Edge remove given edge handle: O(1)
• Edge removal: O(1)
• Vertex insert: amortized O(1)
• Vertex delete: not easily supported

How could we represent Adjacency Matrices in Java?

Topological sorting

Makefile example for building software (a) zig.cpp (b) boz.h (c) zag.cpp (d) zig.o (e) zag.o (f) libzigzag.a

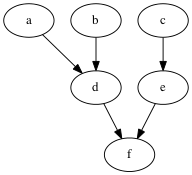
• Is this a well-formed dependence graph, are there any cycles?
• In what order should they be compiled?
• How many steps are required to compile everything in parallel?

Recall that a topological ordering is an ordering A of the vertices such that if A[i] -> A[j], then i < j.

In other words, a vertex needs to come before every other vertex that depends on it.

Here are many (all?) of the topological orderings:

a,b, c, d,e, f
b,a, c, d,e, f
a,b, c, e,d, f
b,a, c, e,d, f
a,b, d, c,e, f
b,a, d, c,e, f
c,e, a,b, d, f
c,e, b,a, d, f

Knuth’s version of Kahn’s algorithm for topological sort

static <V> void topo_sort(Graph<V> G, 
                          Consumer<V> output,
                          Map<V,Integer> num_pred) {
    // initialize the in-degrees to zero
    for (V u : G.vertices()) {
        num_pred.put(u, 0);
    }
    // compute the in-degree of each vertex
    for (V u : G.vertices())
        for (V v : G.adjacent(u))
            num_pred.put(v, num_pred.get(v) + 1);

    // collect the vertices with zero in-degree
    LinkedList<V> zeroes = new LinkedList<V>();
    for (V v : G.vertices())
        if (num_pred.get(v) == 0)
            zeroes.push(v);

    // The main loop outputs a vertex with zero in-degree and subtracts
    // one from the in-degree of each of its successors, adding them to
    // the zeroes bag when they reach zero.
    while (zeroes.size() != 0) {
        V u = zeroes.pop();
        output.accept(u);
        for (V v : G.adjacent(u)) {
        num_pred.put(v, num_pred.get(v) - 1);
        if (num_pred.get(v) == 0)
            zeroes.push(v);
        }
    }
}

Time Complexity of Topological Sort (Knuth’s version)

1. Compute in-degrees

   Outer loop processes every vertex: O(n)

   Outer + inner loop processes every edge: O(m)

   Total: O(n + m)

2. Collect vertices with zero in-degree: O(n)

3. Main loops (while + for) processes each edge just once: O(m)

Total: O(n + m) or because m in O(n²), total is O(n²).

Student Exercise

topologically sort the following graph

V = { belt, jacket, pants, socks, shoes, shirt, tie, undershorts, watch }

E = { belt -> jacket,
      pants -> shoes, pants -> belt,
      socks -> shoes,
      shirt -> tie, shirt -> belt,
      tie -> jacket,
      undershorts -> pants, undershorts -> shoes }

solution: (one of many)

socks, undershorts, pants, shoes, watch, shirt, belt, tie, jacket