Minimum Spanning Trees and Kruskal’s Algorithm

Suppose you’re a cable company and you are planning where to place cables so that you reach every house, but you’d like to minimize the amount of cable that you use.

Definition. A spanning tree is a subset of edges of a graph that form a tree and that connect all the vertices in the graph.

Definition. Given an edge-weighted graph G, the minimum spanning tree problem is to find a spanning tree of G whose total weight is less or equal to any other spanning tree. We write T₁ ≤ T₂ when the total weight of the edges in tree T₁ is less-than or equal to the total weight of the edges in tree T₂.

There are two popular algorithms for MST, I’ll cover the first. The second is in the textbook.

• Kruskal’s, resembles the union-find based connected components
• Prim’s, resembles Dijkstra’s algorithm (see textbook)

The two algorithms have a lot in common.

• They both maintain the following invariant at each step: they’ve identified a set of edges A that is a subset of one or more MSTs.
• At each step, they grow the set A by adding a safe edge (u,v) such that A ∪ {(u,v)} is a subset of one or more MSTs.

But how do we find a safe edge?

We’ll need some definitions to lead up to the answer.

Definitions. Suppose G = (V,E) is a graph with weighted edges.

• A cut is a partition of the vertices into two groups. One can specify a cut with a set of vertices S. The other group is then V - S.
• An edge crosses the cut if one end is in one group and the other edge is in a different group.
• An edge is a light edge if it crosses the cut and its weight is less or equal any other edge that crosses the cut.
• A cut respects a set A of edges if no edge in A crosses the cut.

The following theorem tells us that to find a safe edge, it suffices to find a light edge.

Theorem 23.1 Let A be a subset of some MST of G=(V,E). Let (S,V-S) be a cut of G that respects A. Let (u,v) be a light edge wrt. the cut. Then (u,v) is a safe edge.

Proof. Let T be a MST of G that includes A.

• Case (u,v) in T: Then trivially, A ∪ {(u,v)} ⊆ T.

• Case (u,v) not in T:

  We’re going to construct another MST T’ such that A ∪ {(u,v)} ⊆ T’.

  Because T is spanning, u and v are in T, so there is already a path from u to v in T. Thus, (u,v) completes a cycle. Recall the premise that (u,v) crosses the cut (S,V-S). A cycle with a crossing edge must have another crossing edge as shown in the following diagram. Let that other crossing edge be (x,y) .

       u - - - x
       |       |
    ----------------- cut
       |       |
       v - - - y
  

  We form the new MST T’ by removing (x,y) and adding (u,v):

  T’ = T - {(x,y)} ∪ {(u,v)}

  Now we need to show that T’ is an MST. We know that T’ ≤ T because (u,v) is a light edge, so its weight is less-or-equal to that of (x,y). So T’ is an MST.

  It remains to show that (u,v) is a safe edge, that is,

  A ∪ {(u,v)} ⊆ T - {(x,y)} ∪ {(u,v)}

  We had A ⊆ T, so we need to prove that (x,y) not in A, but we have that because the cut respects A.

QED

We can think of MST algorithms as maintaining a forest of trees, where all the tree edges are in the set A. Initially, each vertex is in it’s own tree because A={}. At each step, we merge two trees into a single tree by identifying the lightest edge connecting them (such an edge is safe).

Kruskal’s Algorithm

Main idea: process all the edges from lightest to heaviest

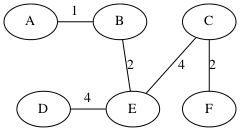
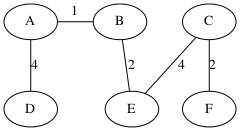
Demo of Kruskal’s algorithm

sorted list of edges:
A-1-B, B-2-E, C-2-F, A-3-E, D-4-E, A-4-D, D-4-B, C-4-E, E-7-F

• Process A-1-B, union {A} and {B}:

        A--B  C
  
        D  E  F
  

• Process B-2-E, union {A,B} and {E}

        A--B  C
           |
        D  E  F
  

• Process C-2-F, union {C} and {F}

        A--B  C
           |  |
        D  E  F
  

• Process A-3-E, do nothing

• Process D-4-E, union {A,B,E} and {D}

        A--B  C
           |  |
        D--E  F
  

• Process A-4-D, do nothing

• Process D-4-B, do nothing

• Process C-4-E, union {A,B,D,E} and {C,F}

        A--B  C
           | /|
           |/ |
        D--E  F
  

Implementation Ideas

• sort the edges by increasing weight to make it easy to process lighter edges before heavier edges.

• use union-find (aka DisjointSets) to keep track of the trees. Recall how DisjointSets works:

  • We represent each partition as a tree whose root is the representative.
  • The tree is stored just in terms of “parent” pointers.
  • sets.make_set(x) sets the parent pointer of x to x.
  • sets.find_set(x) walks up the parent pointers to the root.
  • sets.union(x,y) sets the parent point of x to y (or vice versa).

Implementation of Kruskal’s algorithm in Java

static <V> void kruskal_mst(EdgeGraph<V> G, 
                            Map<V,Map<V,Double>> weight,
                            ArrayList<Edge<V>> T, 
                            DisjointSets<V> sets)
{
    for (V v : G.vertices())
        sets.make_set(v);
    ArrayList<Edge<V>> edges = new ArrayList<Edge<V>>();
    for (Edge<V> e : G.edges())
        edges.add(e);
    sort(edges, new CompareWeight<V>(weight));
    for (Edge<V> e : edges) 
        if (sets.find(e.source()) != sets.find(e.target())) {
            T.add(e);
            sets.union(e.source(), e.target());
        }
}

Time complexity

• initialize disjoint sets: O(n α(n))
• sort: O(m log m)
• main loop: O(m α(n))

The dominating cost is the sorting. So the overall time complexity is O(m log m) which can be instead stated as O(m log n) because m < n² and therefore log m < 2 log n.

Student group work

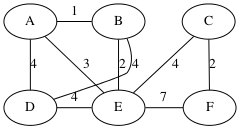
apply Kruskal’s to the following graph (didn’t get to this)

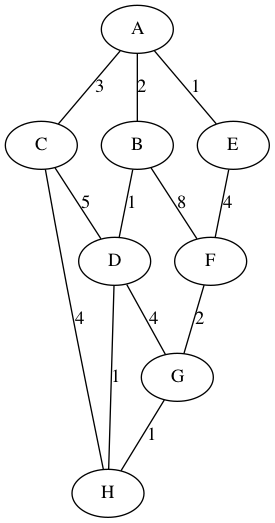
Solution: sorted edges:

	   A-1-E, G-1-H, B-1-D, D-1-H
	   F-2-G, A-2-B, 
	   A-3-C,
	   E-4-F, C-4-H, D-4-G
	   C-5-D, 
	   B-8-F

An MST of weight 11: (there are other MST’s)