Lecture: Shortest Paths

We have seen the shortest path problem where each edge counts as distance 1 and we used BFS to solve it. Now we consider graphs where each edge has a real number for its weight.

Notation: We write w(u,v) or w(e) for the weight of an edge.

Definition The weight of a path is the sum of the weights of its edges. We also use the term distance for the weight of a path.

So for path p = e₁, e₂, …, eᵣ

w(p) = Σ{i∈1..r} w(eᵢ)

Motivation for the shortest path problem:

• internet packet routing
• driving routes
• minimizing flight duration

As with BFS, we’ll focus on the single-source shortest-paths problem: finding the shortest path from a source vertex to every other vertex in the graph. Other alternatives are:

• Single-destination shortest-paths
• Single-pair shortest-path
• All-pairs shortest-paths

Algorithm Preview

• Bellman-Ford: O(nm)
• Disjktra:
  • using min-heap: O((n+m) log(n))
  • using Fibonnaci heap: O(n log(n) + m)
• DAG Shortest: O(n+m) (uses topological sort)

Brute force: compute the length of every path

But this is exponential time: there are O(2^n) paths. Here’s a worst-case scenario.

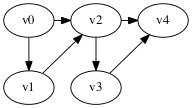
Shortest paths exhibit optimal substructure

That is, a subpath of a shortest path is a shortest path.

More precisely, if you have a shortest path

v₀ →ᵣ vᵢ →p vⱼ →q vk

then the subpath p

vᵢ →p vⱼ

is a shortest path from vᵢ to vⱼ.

Proof. Suppose vᵢ →p vⱼ is not a shortest path from vᵢ to vⱼ. Then we splice the shortest path p’ from vᵢ to vⱼ into the path v₀ → vk to get

v₀ →ᵣ vᵢ →p' vⱼ →q vk

which is a shorter path from v₀ to vk. But that contradicts the assumption that

v₀ →ᵣ vᵢ →p vⱼ →q vk

was a shortest path.

Take away: we can build shortest paths by growing them from smaller shortest paths.

Notation: d(u,v) is the weight of the shortest path from u to v.

Negative-weight edges

Motivation: weak, not very common

Some shortest-path algorithms handle this (Bellman-ford), some do not (Dijkstra, DAG Shortest Paths).

None of them handle graphs with negative-weight cycles, as the notion of shortest-path doesn’t make sense on such graphs.

Example:

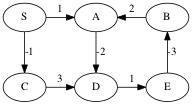
The shortest path from S to C is -1.

The shortest path from S to A is undefined because you can keep going around the cycle A → D → E → B, which has weight -2.

We can avoid negative weights in some situations by shifting weights up.

Triangle Inequality

For all edges u → v, d(s,v) ≤ d(s,u) + w(u,v).

Proof: s → u → v is a path from s to v, and d(s,v) is the weight of the shortest path.

Relaxation

We maintain a current best path length, an upper bound, on the distance to a vertex.

We relax an edge by updating the distance of the target vertex if this edge provides a shorter path to it.

static void relax(Edge e, double[] distance, int[] parent,
                  Map<Edge,Double> weight) {
    if (distance[e.target] > distance[e.source] + weight.get(e)) {
	    distance[e.target] = distance[e.source] + weight.get(e);
		parent[e.target] = e.source;
	}
}

Dijkstra Shortest Paths

Like BFS, the idea is to expand the wavefront of shortest-paths so far.

The challenge is to figure out how to explore paths in the order of their weight. Consider the following graph with the source vertex S.

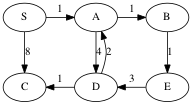
Growing the shortest paths tree in order of path weight:

        W=0   S

        W=1   S-->A


        W=2   S-->A-->B


        W=3   S-->A-->B
                      |
                      V
                      E

        W=5   S-->A-->B
                  |   |
                  V   V
                  D   E

        W=6   S-->A-->B
                  |   |
                  V   V
              C<--D   E

Dijkstra’s solution is to store all the potential next vertices (those that are adjacent to the tree) in a priority queue ordered by their distance as computed by the current tree plus the weight of the lightest edge to that vertex. Then the minimum of the priority queue gives the next shortest path.

               SPT                  Priority Queue
        W=0    S                    A:1, C:8

        W=1    S---A                B:2, D:5, C:8

        W=2    S---A---B            E:3, D:5, C:8

        W=3    S---A---B            D:5, C:8
                       |
                       |
                       E

        W=5    S---A---B            C:6  (decrease key!)
                   |   |
                   |   |
                   D   E

        W=6    S---A---B
                   |   |
                   |   |
               C---D   E

Student group work: use Dijkstra’s to compute the distances from S to all the other vertices in the following graph.

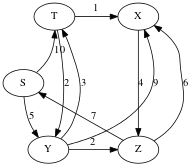
    Answers:

           S: 0
           T: 8
           X: 9
           Y: 5
           Z: 7

Time Complexity of Dijkstra’s Algorithm

• n pushes to the queue: O(n log(n))
• n pops from the queue: O(n log(n))
• m decrease_key on the queue: O(m log(n))
• Total: O((n+m) log(n))